من خلال الأنشطة التقديمية للمعادلات الواردة في هذه (الصفحة : مقدمة للمعادلات) و هذه (الصفحة : أنشطة حول المعادلات) يتضح أن هناك معادلتان أساسيتان الأولى على شكل a + x = b و الثانية على شكل ax = b. هذا الدرس يشرح طريقة حل المعادلة a + x = b :
1- المعادلة : x + a = b
تعريـــف :
a و b و x أعداد حقيقية .
كل متساوية على شكــل : x + a = b تسمى معادلة من الدرجة الأولى بمجهول واحد هو x.- x + 2 =7 هي معادلة ذات المجهول x ولدينا : x = 7 - 2 = 5. إذن : حل هذه المعادلة هو 5
- y - 5 = 20,5 هي معادلة ذات المجهول y ولدينا : y = 20,5 + 5 = 25,5. إذن : حل هذه المعادلة هو 25,5
2- طريقة حل المعادلة : x + a = b
قاعدة :
في متساوية يمكن أن نضيف (أو نطرح) من طرفيها نفس العدد دون أن تتغير هذه متساوية.| سنقصي العدد "2-" من الطرف الأيسر | نضيف إليه 2+ | نحسب طرف بطرف : | نحصل على : | حل المعادلة هو |
 |
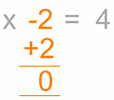 |
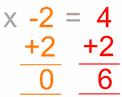 |
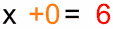 |
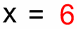 |
| المعادلة في حالتها الأصلية | نضيف 2 فقط الى الطرف الأيسر | عندما نضيف 2 إلى طرفي المعادلة |
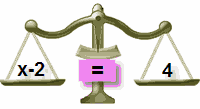 |
 |
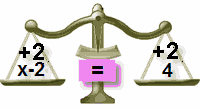 |
| الميزان في حالة توازن | الميزان في حالة عدم توازن | الميزان في حالة توازن |
حل المعادلات التالية :
- x + 9 = 15
- x - 6 = 3,5
- 5x
+1,2 = 6x
| المعادلة رقم | إرشادات | الإنجاز |
| 1 | لدينا : |
 |
| نطرح 9 من طرفي المعادلة => | ||
| 0 = 9 - 9 و 6 = 9 - 15 | ||
| 2 | لدينا : |
 |
| نضيف 6 إلى طرفي المعادلة => | ||
| 0 = 6 + 6- و 9,5 = 6 + 3,5 | ||
| 3 | لدينا : |  |
| نطرح 5x من طرفي المعادلة => | ||
| 5x - 5x = 0 و 6x - 5x = x |


ليست هناك تعليقات:
إرسال تعليق